2019-07-17发表2020-11-21更新OI / 题解

创世纪

题目概述

上帝手中有 $N \le 10^5$ 种世界元素，每种元素可以限制另外 $1$ 种元素，把第 $i$ 种世界元素能够限制的那种世界元素记为 $A[i]$ 。

现在，上帝要把它们中的一部分投放到一个新的空间中去建造世界。

为了世界的和平与安宁，上帝希望所有被投放的世界元素都有至少一个没有被投放的世界元素限制它。

上帝希望知道，在此前提下，他最多可以投放多少种世界元素？

感觉网上的贪心题解都稍有问题？

单纯考虑一个树（不是基环树），发现可直接从子节点贪心得出父节点状态

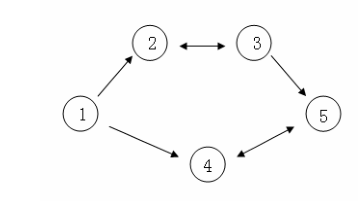
首先，这是一个内向树森林

考虑一颗内向基环树 $T$ ，环上节点为 $s_1, s_2, \cdots,s_t$

对每一个环上节点和其子树分开执行贪心（这只是描述，实际上用拓扑排序递推）

如果 $T$ 是一个环，则 $t/2$
如果存在一个 $s_i$ 由贪心过程得出它可以投放，则环就会断成链
如果不存在，则环还是完整的， $t/2$

贪心过程由拓扑排序执行，讨论 2 可以直接在这个过程中完成

2019-07-16发表2020-11-21更新OI / 学习笔记

树上差分

首先，树上差分是从子节点推到根节点，定义 $d$ 差分数组

若修改 $(x,y)$ 路径上的点权，则 $d_x, d_y \mathrel{+}= k, d_{\mathrm{lca}}, d_{\mathrm{fa}_{\mathrm{lca}}} \mathrel{-}= k$

void dfs(int u){
    val[u] = d[u];
    for (auto v : g[u]){
        dfs(v), val[u] += val[v];
    }
}

若修改 $(x,y)$ 路径上的边权，则 $d_x, d_y \mathrel{+}= k, d_{\mathrm{lca}}\mathrel{-}= 2k$

int dfs(int u){
    int ret = d[u];
    for (auto i : g[u]){
        i.w = dfs(i.v);
        ret += i.w;
    }
    return ret;
}

P3128 最大流

2019-07-15发表2020-11-21更新OI / 题解

Network，闇の連鎖

仔细分析，考虑树上，若断一条树边 $(u, v)$ ，则会分成两个连通块

两个连通块之间有 $0$ 条附加边，则任意再切一条
两个连通块之间有 $1$ 条附加边，则只能切特定的一条
两个连通块之间有 $\geq 2$ 条附加边，无方案

如何快速计数？

记附加边为 $(x,y)$ ，发现 $(u, x),(v,y)$ 两条路径不相交则 $(x,y)$ 对 $(u,v)$ 有影响

即，附加边 $(x,y)$ 对于主要边树上 $(x,y)$ 路径上所有边都有影响

或者说，附加边 $(x,y)$ 会在树上产生环，如果切环上的边就必须把 $(x,y)$ 切掉

然后就是树上边差分

POJ 上 TLE 了，但是本地没问题，复杂度（应该）没挂？

2019-07-14发表2020-11-21更新OI / 学习笔记

求 LCA 的 Tarjan 算法

这是一个复杂度为 $O(n+q)$ 的离线求 LCA 算法

用 dfs 进行遍历并打 tag

假设遍历到 $u$ ，则已回溯的节点标为 $2$ ，遍历到但未回溯的节点（即 $u$ 和 $u$ 的祖先）标 $1$ ，其余为 $0$

现在假设 $u$ 的子树处理完毕，考虑 $u$ 的处理

询问节点为 $(u, v)$

此时，若 $\mathrm{tag}_v = 2$ ，则可以保证 $v$ 向根走遇到的第一个 $\mathrm{tag} = 1$ 的节点即为 $\mathrm{LCA}(u,v)$ ，可以用反证法证明

若向根走遇到的第一个 $\mathrm{tag} = 1$ 的节点，记为 $w$ ， $w \not = \mathrm{LCA}(u,v)$

记 $\mathrm{LCA}(u,v)$ 为 $p$

显然 $p$ 在 $u$ 到根的路径上

若 $p$ 在 $w$ 下方，则 $\mathrm{tag}_p \not= 1$ ，但是 $p$ 又为 $u$ 的祖先， $\mathrm{tag}=1$

矛盾

若 $p$ 在 $w$ 上方，根据算法可得 $w$ 为 $v$ 的祖先，又 $\mathrm{tag}_w = 1$ 得 $w$ 为 $u$ 的祖先，所以 $w$ 必为 $u$ 和 $v$ 的公共祖先，但是 $p$ 是 $w$ 的祖先

矛盾

证毕

下面的程序复杂度应该没有问题，但是要卡一下常，吸一口氧才能过

2019-07-14发表2020-11-21更新OI / 题解

「APIO 2010」巡逻

容易发现，若不加新边，则总距离为 $2(n-1)$

发现 $k=1$ 时，连一条边等于环上的边只需走一次，显然最优连直径

发现 $k=2$ 时，再连一条边，若构成的环和第一次的环不相交，则可以直接减

若相交，则需要经过重叠部分两次，可以通过把边权改成 $-1$ 实现

对于新边能走一次，可以用，不实际在图上加边，来控制

2019-07-12发表2020-11-21更新OI / 题解

「USACO 2011 Jan. Gold」道路和航线

题目概述

LOJ #10081. 「一本通 3.2 练习 7」道路和航线 原题来自：USACO 2011 Jan. Gold

Farmer John 正在一个新的销售区域对他的牛奶销售方案进行调查。他想把牛奶送到 $T$ 个城镇，编号为 $1$ 到 $T$ 。这些城镇之间通过 $R$ 条道路（编号为 $1$ 到 $R$ ）和 $P$ 条航线（编号为 $1$ 到 $P$ ）连接。每条道路 $i$ 或者航线 $i$ 连接城镇 $A_i$ 到 $B_i$ ，花费为 $C_i$ 。

对于道路， $0 \le C_i \le 10^4$ ，然而航线的花费很神奇，花费 $C_i$ 可能是负数。道路是双向的，可以从 $A_i$ 到 $B_i$ ，也可以从 $B_i$ 到 $A_i$ ，花费都是 $C_i$ 。然而航线与之不同，只可以从 $A_i$ 到 $B_i$ 。

事实上，由于最近恐怖主义太嚣张，为了社会和谐，出台了一些政策保证：如果有一条航线可以从 $A_i$ 到 $B_i$ ，那么保证不可能通过一些道路和航线从 $B_i$ 回到 $A_i$ 。由于 FJ 的奶牛世界公认十分给力，他需要运送奶牛到每一个城镇。他想找到从发送中心城镇 $S$ 把奶牛送到每个城镇的最便宜的方案，或者知道这是不可能的。

如果去掉航线可以发现原图变成了许多连通块

若把一个连通块看成一个节点,则发现连通块和航线组成 DAG

考虑 Topo sort 结合 Dijkstra

称连通块和航线组成的图为 $G$ ，连通块 $A$ 内部节点和道路的图为 $g_A$

假设 $s$ 所在的连通块为 $S$ ，对所有在 $G$ 中可从 $S$ 到达的连通块进行拓扑排序（否则算 deg 的时候会算多），一边拓扑一边 Dijkstra

大致是这个样子

q <- Topo_Queue;
while(q not empty):
    clr = q.front(); q.pop();
    
    heap <- Dijkstra_Priority_Queue;
    for (u 为 clr 节点)
        if (dis[u] != INF) heap.push(dis[u], u);
    
    while(heap not empty):
        u = heap.top(); heap.pop();
        for 从 u 出发道路:
            // 普通 Dijkstra 写法，略
        for 从 u 出发的航线(u, v, w):
            A 为 v 所在的连通块;
            if (A 不可从 S 出发到达) continue;
            deg[A]--;
            if (deg[A] == 0) q.push(A);
            dis[v] = min(dis[v], dis[u] + w)

2019-07-12发表2020-11-21更新OI / 题解

「NOIP 2009」最优贸易

题目概述

LOJ #2590. 「NOIP2009」最优贸易 C 国有 $n$ 个大城市和 $m$ 条道路，每条道路连接这 $n$ 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 $m$ 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 $1$ 条。

C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 C 国 $n$ 个城市的标号从 $1\sim n$ ，阿龙决定从 $1$ 号城市出发，并最终在 $n$ 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有 $n$ 个城市。

阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品——水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设 C 国有 $5$ 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

假设 $1$ ~ $n$ 号城市的水晶球价格分别为 $4,3,5,6,1$ 。

阿龙可以选择如下一条线路： $1\to 2\to 3\to 5$ ，并在 $2$ 号城市以 $3$ 的价格买入水晶球，在 $3$ 号城市以 $5$ 的价格卖出水晶球，赚取的旅费数为 $2$ 。

阿龙也可以选择如下一条线路 $1\to 4\to 5\to 4\to 5$ ，并在第 $1$ 次到达 $5$ 号城市时以 $1$ 的价格买入水晶球，在第 $2$ 次到达 $4$ 号城市时以 $6$ 的价格卖出水晶球，赚取的旅费数为 $5$ 。

现在给出 $n$ 个城市的水晶球价格， $m$ 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

¶ 解法一

Tarjan 缩点，重构图 + 判可达性（某一个强连通分量能否到达终点，若不能，则不能更新 ans ） + 跑 DAG 上的 DP

用了一个结论：Tarjan 逆序即为拓扑序

具体看代码吧

#include <algorithm>
#include <cassert>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <deque>
#include <iostream>
#include <map>
#include <queue>
#include <set>
#include <stack>
#include <string>
#include <utility>
#include <vector>
#define rep(i, l, r) for (int i = (l); i <= (r); ++i)
#define per(i, l, r) for (int i = (l); i >= (r); --i)
using std::cerr;
using std::cin;
using std::cout;
using std::endl;
using std::make_pair;
using std::pair;
typedef pair<int, int> pii;
typedef long long ll;
typedef unsigned int ui;

const int N = 100005;

std::vector<int> g[N], ng[N], fg[N];
int price[N];

int min[N], max[N], dfn[N], ins[N], low[N], color[N], dp[N];
std::stack<int> s;
int cnt = 0;
int T = 0;

void tarjan(int u) {
    dfn[u] = low[u] = ++T, ins[u] = 1;
    s.push(u);
    for (auto v : g[u]) {
        if (!dfn[v]) {
            tarjan(v);
            low[u] = std::min(low[u], low[v]);
        } else if (ins[v]) {
            low[u] = std::min(low[u], low[v]);
        }
    }
    if (dfn[u] == low[u]) {
        int x;
        cnt++;
        // cerr << "cnt" << cnt << ":\n";
        do {
            x = s.top();
            s.pop();
            // cerr << x << ' ';
            color[x] = cnt, ins[x] = 0;
            min[cnt] = std::min(min[cnt], price[x]);
            max[cnt] = std::max(max[cnt], price[x]);
        } while (x != u);
        // cerr << endl;
    }
}

int coutable[N];

void dfs(int u) {
    if (coutable[u]) return;
    coutable[u] = 1;
    for (auto v : fg[u]) dfs(v);
}

int main() {
#ifdef LOCAL
    freopen("input", "r", stdin);
#endif
    std::memset(min, 0x3f, sizeof(min));
    std::ios::sync_with_stdio(false);
    cout.tie(0);
    int n, m;
    cin >> n >> m;
    rep(i, 1, n) cin >> price[i];
    rep(i, 1, m) {
        int x, y, z;
        cin >> x >> y >> z;
        g[x].push_back(y);
        if (z - 1) g[y].push_back(x);
    }

    // tarjan
    tarjan(1);

    // rebuild
    rep(u, 1, n) {
        for (auto v : g[u])
            if (color[u] != color[v]) ng[color[u]].push_back(color[v]);
    }

    // connectable
    rep(u, 1, cnt) for (auto v : ng[u]) fg[v].push_back(u);
    dfs(color[n]);

    // topo + dp
    int ans = 0;
    std::memset(dp, 0x3f, sizeof(dp));
    per(u, cnt, 1) {
        dp[u] = std::min(dp[u], min[u]);
        if (coutable[u]) ans = std::max(ans, max[u] - dp[u]);
        for (auto v : ng[u]) {
            dp[v] = std::min(dp[v], dp[u]);
        }
    }

    cout << ans;
    return 0;
}

¶ 解法二

正图反图跑 SPFA转移方程定义为

d_{v} = \min\Big(\min_{u\rightarrow v}\{d_u\}, price_v\Big)

最后减一下

¶ 解法三

引用一下

构造分层图，具体看上面

2019-05-18发表2020-11-21更新OI / 学习笔记

Miller Rabin 判素

¶ 数学

¶ 费马小定理

对于素数 $p$ 必存在

a^{p-1} \equiv 1 \pmod{p}

所以可以随机选取 $a\in[2,n-1]$ 检验是否满足上式，若不满足，则必然是合数

遗憾的是，存在无穷多个 $n$ ，可以满足

\forall\ x\in[2,n-1]\\ x^{n-1}\equiv 1 \pmod{n}

也就是说使费马判素失效

¶ 二次探测定理

素数 $p$ 必满足方程

x^2\equiv1\pmod{p}

有且仅有两个解

x_1\equiv1,\ x_2\equiv p-1\pmod{p}

¶ 实现

把 $n-1$ 分解成 $d\cdot2^t$ 使 $t$ 尽量大

然后 $x\equiv base^{d} \pmod{n}$

然后不断进行二次探测

即如果满足 $x\not\equiv 1$ 且 $x\not\equiv n-1$ 且 $x^2\equiv 1$ 那么这个数解不是素数了

最后进行费马判素

bool miller_rabin(ll n) {
    if (n <= 2) return n == 2;
    int d = n - 1, t = 0;
    while (d % 2 == 0) d /= 2, ++t;
    rep(i, 0, T) { // T 是测试次数, p 是测试基
        ll x = ksm(p[i] % (n - 2) + 2, d, n);
        if (x == 1 || x == n - 1) continue; // 无效的二次探测
        for (int j = 0; j < t; ++j, x = x * x % n)
            if (x != n - 1 && x != 1 && x * x % n == 1) return 0;
        if (x != 1) return 0; // 费马判素
    }
    return 1;
}

这是测试基选择的推荐

数据范围	测试基
$2^{32}$	2,7,61
$2^{64}$	2,3,5,7,11,13,17,19,23,29,31,37

2019-05-11发表2020-11-21更新OI / 题解

「一本通 1.1 练习 4」家庭作业题解

题目概述

LOJ #10008. 「一本通 1.1 练习 4」家庭作业

老师在开学第一天就把所有作业都布置了，每个作业如果在规定的时间内交上来的话才有学分。每个作业的截止日期和学分可能是不同的。例如如果一个作业学分为 $10$ ，要求在 $6$ 天内交，那么要想拿到这 $10$ 学分，就必须在第 $6$ 天结束前交。

每个作业的完成时间都是只有一天。例如，假设有 7 次作业的学分和完成时间如下：

作业号	期限	学分
$1$	$1$	$6$
$2$	$1$	$7$
$3$	$3$	$2$
$4$	$3$	$1$
$5$	$2$	$4$
$6$	$2$	$5$
$7$	$6$	$1$

最多可以获得 $15$ 学分，其中一个完成作业的次序为 $2,6,3,1,7,5,4$ ，注意可能还有其他方法。

你的任务就是找到一个完成作业的顺序获得最大学分。

显然的贪心，先按学分 $s$ 从大到小，再按期限 $d$ 从后到前

考虑要安排一个作业，显然是越晚越好，故用一个二分区间，用一个数据结构查询、修改

这里选择二分套树状数组

2019-05-05发表2020-11-21更新OI / 学习笔记

粒子群算法

¶ 概述

这是一种随机算法

模仿鸟类捕食

在定义域中随机撒 $n$ 个点，需要维护（以二维定义域为例）

坐标 $p(x,y)$
速度 $v$ ，一个二维向量
历史最优值 $pb$ 和其坐标

同时还要维护全局最优解及其坐标

创世纪

树上差分

Network，闇の連鎖

求 LCA 的 Tarjan 算法

「APIO 2010」巡逻

「USACO 2011 Jan. Gold」道路和航线

「NOIP 2009」最优贸易

¶ 解法一

¶ 解法二

¶ 解法三

Miller Rabin 判素

¶ 数学

¶ 费马小定理

¶ 二次探测定理

¶ 实现

「一本通 1.1 练习 4」家庭作业题解

粒子群算法

¶ 概述

分类

标签

作业号	期限	学分
$1$	$1$	$6$
$2$	$1$	$7$
$3$	$3$	$2$
$4$	$3$	$1$
$5$	$2$	$4$
$6$	$2$	$5$
$7$	$6$	$1$

作业号	期限	学分
$1$	$1$	$6$
$2$	$1$	$7$
$3$	$3$	$2$
$4$	$3$	$1$
$5$	$2$	$4$
$6$	$2$	$5$
$7$	$6$	$1$

作业号	期限	学分
$1$	$1$	$6$
$2$	$1$	$7$
$3$	$3$	$2$
$4$	$3$	$1$
$5$	$2$	$4$
$6$	$2$	$5$
$7$	$6$	$1$