定义
定义一
∣F1P∣+∣F2P∣=2a∣F1F2∣=2ca2x2+b2y2=1(a>b>0)∣PF1∣=a+ex∣PF2∣=a−ex定义二
定义三

d=∣AA1∣d∣F2P∣=e<1通径∣CD∣=2ab2∣F2M∣=p=ca2−c=cb2∣AF2∣=1+ecosθep∣BF2∣=1−ecosθep∣AB∣=1−e2cos2θ2ep∣BF2∣∣AF2∣=1+ecosθ1−ecosθ注意,通过控制 θ 可以得出 ∣AB∣min=2ab2
乱七八糟
三角换元
a2x2+b2y2(ax)2+(by)2=1=1{x=a⋅cosαy=b⋅sinα点差法
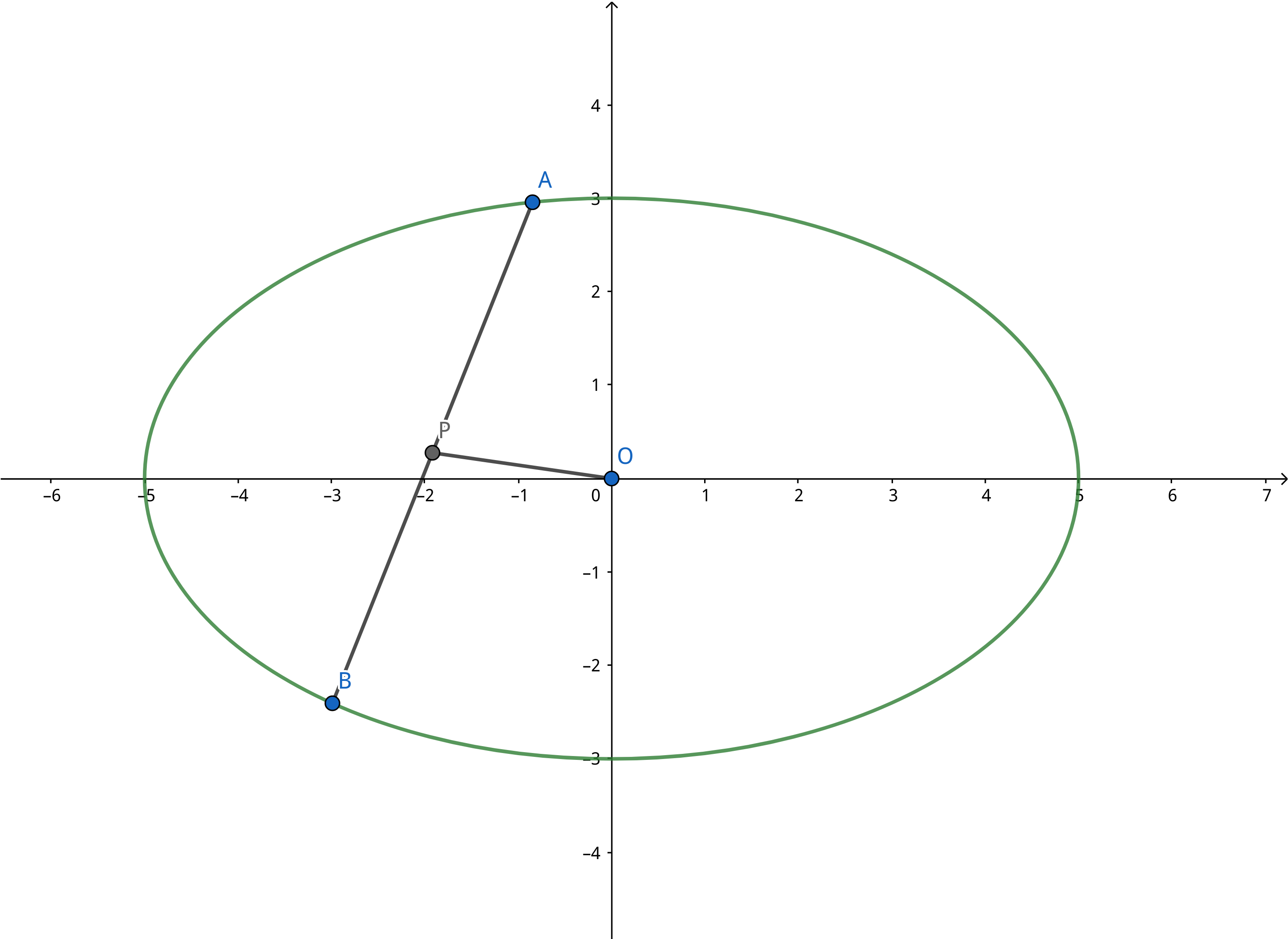
⎩⎪⎪⎪⎨⎪⎪⎪⎧a2x12+b2y12=1a2x22+b2y22=1a2x12−x22x1−x2y1−y2⋅x1+x2y1+y2x1−x2y1−y2⋅x0y0kAB⋅kOP=−b2y12−y02=−a2b2=−a2b2=−a2b2切线
Ax2+By2+Cx+Dy+E=0Ax0x+By0y+C2x0+x+D2y0+y+E=0整体思想
x1+kx2=0x2x1=−kx1x2=−k1x2x1+x1x2=x1x2x12+x22=x1x2(x1+x2)2−2x1x2(x1+x2)2=−k−k1+2焦点三角形
仿射变换

