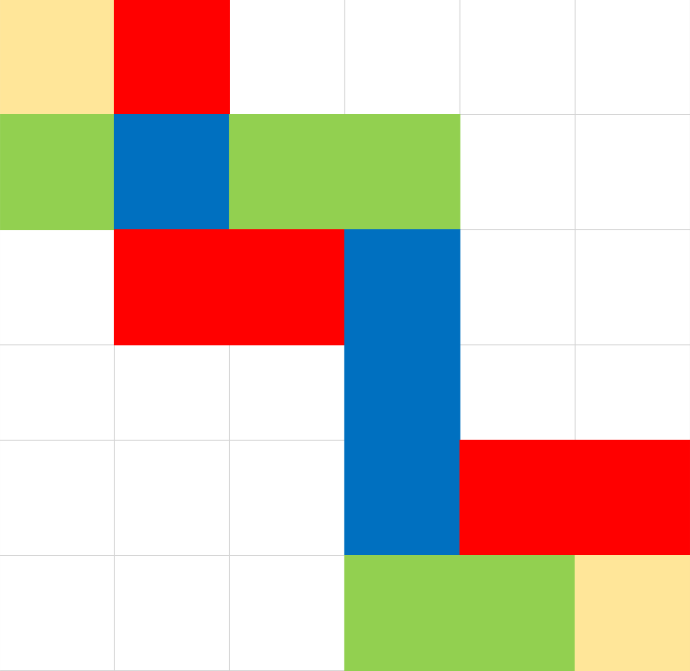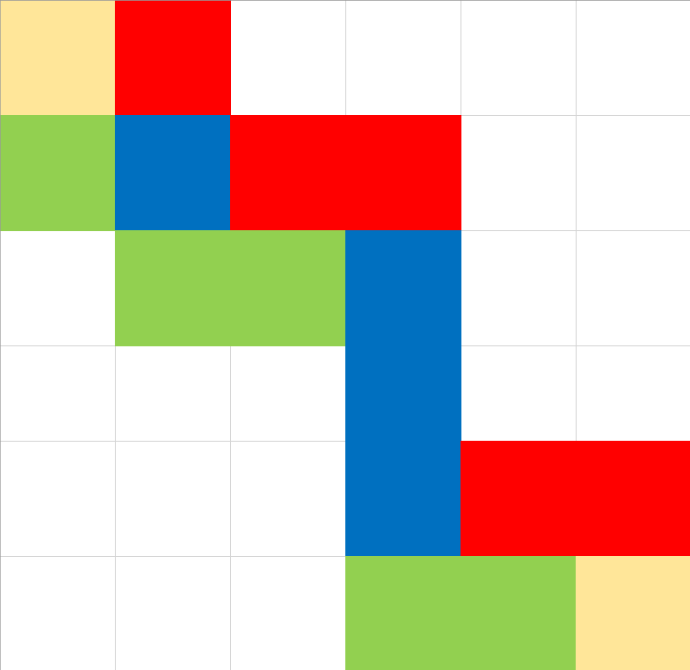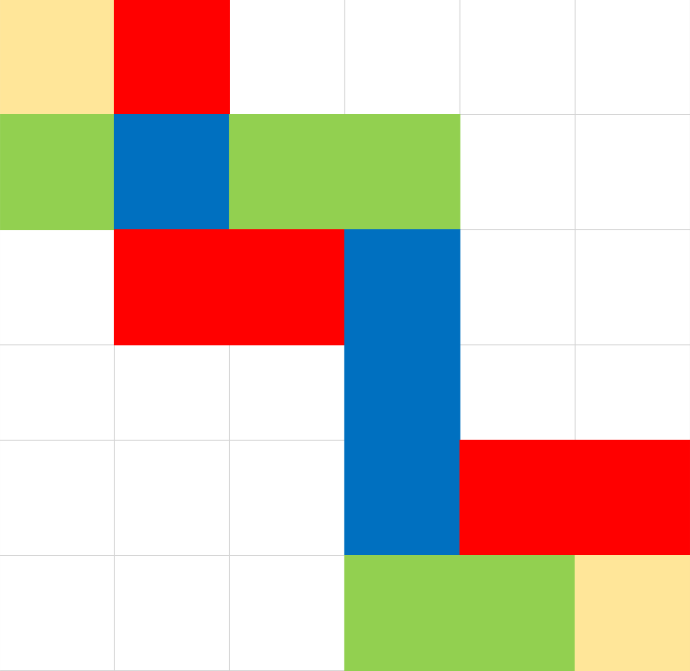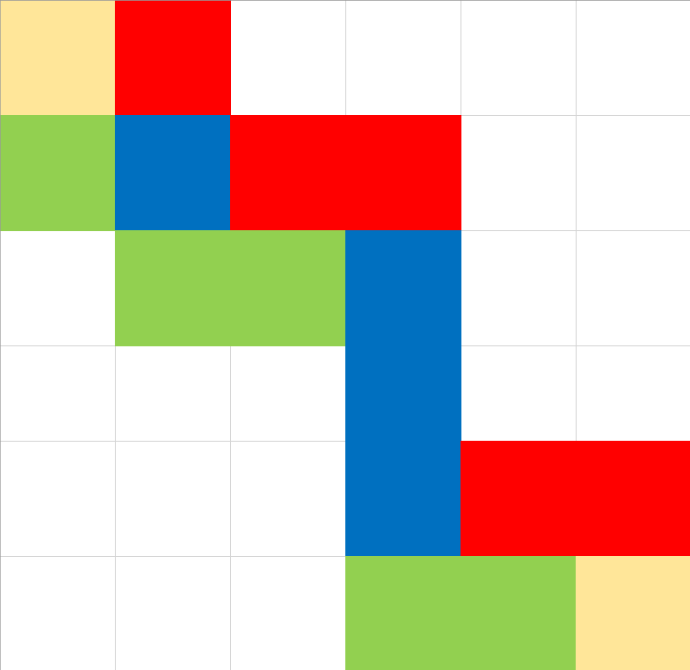「NOIP 2008」传纸条

题目链接

为了方便，坐标先行后列。

设 $A = (1, 1),B = (m, n)$

不考虑不能传相同同学

从 A 到 B 再从 B 到 A $\sim$ 从 A 同时考虑两条路到 B

设 $i$为 A 到 B 线路 1 的行号，$j$为 A 到 B 线路 2 的行号，$k$为当前行列之和

对于线路1，$(i, k-i)$ 可从 $(i-1, k-i)$ 和 $(i, k-i-1)$ 推得

对于线路2，$(j, k-j)$ 可从 $(j-1, k-j)$ 和 $(j, k-j-1)$ 推得

故对于 $dp(i, j, k)$ 有四种情况。

$$\begin{aligned} dp(i, j, k) = a[i][k-i] + a[j][k -j] + \max\{ & dp(i, j, k-1), \\ & dp(i-1,j-1,k-1), \\ & dp(i-1,j,k-1), \\ & dp(i-1,j-1,k-1)\} \\ \end{aligned}$$

现在来考虑重合。红绿为两条路线，蓝色为相交部分。

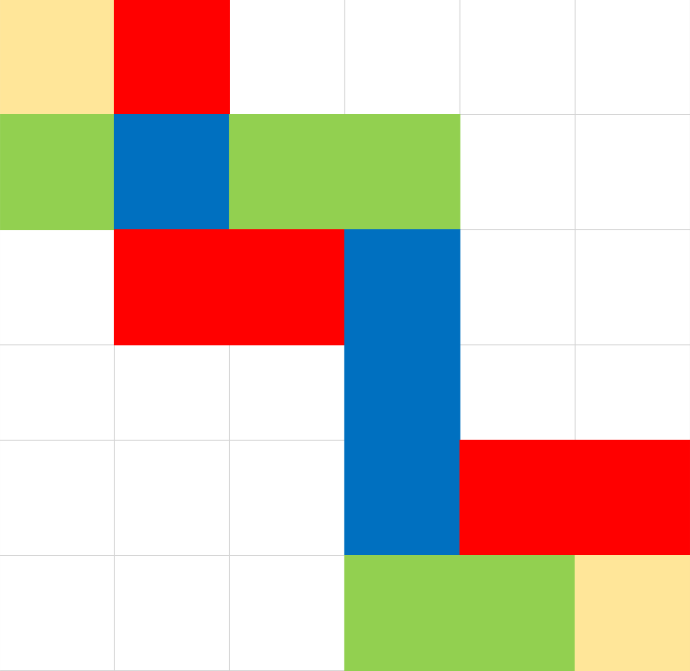
经过变换，可以变成这样。

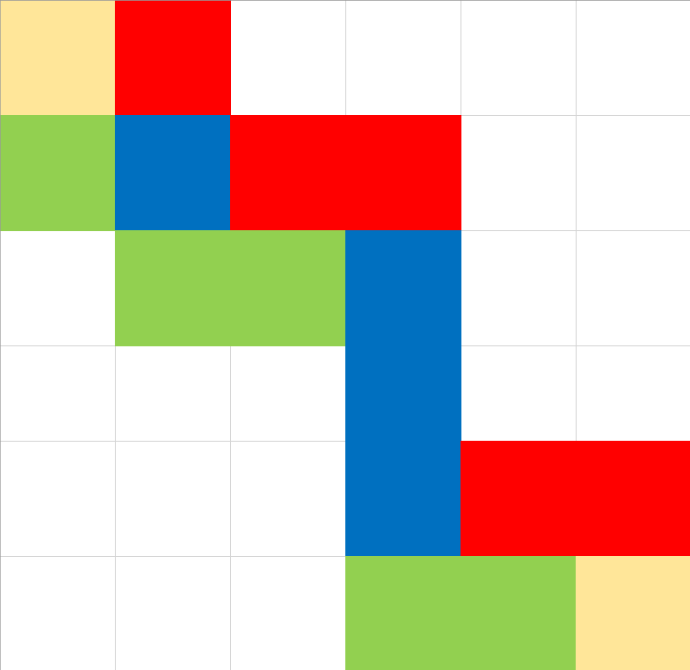
现在问题主要是解决蓝色格子，由于两条路线规划同时从左上角开始，代码实现时 k->i->j 三重循环。

若$i=j$那么就是有重叠，此时只要把多的一次减掉。

$\because$ 对于某一条路线来说，走了一个价值为 $0$ 的格子的路线。

又 $\because a_{i,j} \ge 0$

$\therefore$ 必定没有一种不相交的路线规划比起更劣。

$\therefore$ 此重叠的方案不会是最优方案，必定会在动规中舍弃。

比如绿色路线可以是 $(2,1)(3,1) (2,2)(3,3)(4,3)(5,3)(6,3)(6,4)(6,5)$

cin >> m >> n;
for (register int i = 1; i <= m; ++i){
    for (register int j = 1; j <= n; ++j){
        cin >> a[i][j];
    }
}
for (register int k = 3; k <= m + n; ++k){
    t1 = min(k-1, m);
    for (register int i = 1; i <= t1; ++i){
        t2 = min(k-1, m);
        for (register int j = 2; j <= t2; ++j){
            dp[i][j][k] = max(
                dp[i-1][j][k-1],
                dp[i-1][j-1][k-1],
                dp[i][j-1][k-1],
                dp[i][j][k-1]
            ) + a[i][k-i] + a[j][k-j];
            if (i == j) dp[i][j][k] -= a[i][k-i];
       }
    }
}
cout << dp[m][m][m+n];