发表更新OI

初赛复习

知识点

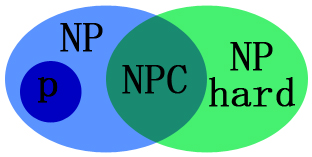
  • P Problem: 对于任意的输入规模n，问题都可以在n的多项式时间内得到解决；
  • NP(Non-deterministic Polynomial) Problem: 可以在多项式的时间里验证一个解的问题；
  • NPC(Non-deterministic Polynomial Complete) Problem: 满足两个条件 (1)是一个NP问题 (2)所有的NP问题都可以约化到它
  • NP-Hard Problem: 满足NPC问题的第二条，但不一定要满足第一条

（ AB ）属于 NP 类问题。

  • 存在一个 P 类问题
  • 任何一个 P 类问题
  • 任何一个不属于 P 类的问题
  • 任何一个在（输入规模的）指数时间内能够解决的问题

主定理

T(n)=aT(n/b)+f(n) T(n)=aT(n/b)+f(n)

考虑 A(n)=nlog⁡baA(n)=n^{\log_b a} 和 f(n)f(n) 的大小

  • f(n)<A(n)f(n)<A(n) ， O(A(n))O(A(n))
  • f(n)=A(n)log⁡knf(n)=A(n)\log^k n ， O(A(n)log⁡k+1n)O(A(n)\log^{k+1}n)
  • f(n)>A(n),∃  c<1,af(n/b)<cf(n)f(n)>A(n),\exist\;c<1, af(n/b)<cf(n) ， O(f(n))O(f(n))

原反补

补=反+1

原地排序、稳定排序、复杂度

特殊二叉树定义

  • 满二叉树(Full Binary Tree)： 要么是叶子结点(结点的度为0)，要么结点同时具有左右子树(结点的度为2)
  • 完全二叉树(Complete Binary Tree)： 每层结点都完全填满，在最后一层上如果不是满的，则只缺少右边的若干结点。
  • 完美二叉树(Perfect Binary Tree) 所有的非叶子结点都有两个孩子，所有的叶子结点都在同一层。即每层结点都完全填满。

完全二叉树共有2*N-1个结点，则它的叶节点数是（ C ）。

A. N-1 B. 2*N C. N D. 2N-1 E. N/2

排列组合

书架上有21本书，编号从1到21，从其中选4本，其中每两本的编号都不相邻的选法一共有___3060___种。

∑i=15ai=21−4=17a1,a5≥0,a2,a3,a4>0(17+2−15−1)=3060 \begin{aligned} \sum_{i=1}^5 a_i = 21-4=17\\ a_1,a_5\ge 0, a_2,a_3,a_4>0\\ \binom{17+2-1}{5-1}=3060 \end{aligned}

1,1,2,4,8,8 组成的不同四位数个数：102

错排 Dn=(n−1)(Dn−2+Dn−1)D_n = (n-1)(D_{n-2}+D_{n-1})

特征根

f0=0,f1=1,fn+1=(fn+fn−1)/2f_0=0, f_1=1,f_{n+1}=(f_n+f_{n-1})/2

lim⁡n→∞fn=?\lim_{n\rightarrow\infin} f_n=?

欧拉图/欧拉路

  • 欧拉路：不重不漏经过每一条边
    恰好有两个点度数为奇
  • 欧拉回路：存在欧拉路起点重点相同
  • 欧拉图 G 是指可以构成一个闭回路的图
    每个点度数为偶

，且图G的每一条边恰好在这个闭回路上出现一次（即一笔画成）。在以下各个描述中, 不一定是欧拉图的是：（   D   ）。

  • 图G中没有度为奇数的顶点
  • 包括欧拉环游的图(欧拉环游是指通过图中每边恰好一次的闭路径)
  • 包括欧拉闭迹的图(欧拉迹是指通过途中每边恰好一次的路径)
  • 存在一条回路, 通过每个顶点恰好一次
  • 本身为闭迹的图

图灵停机

一个无法靠自身的控制终止的循环称为“死循环”，例如在C语言程序中，语句“while(1)printf("")；”就是一个死循环，运行它将无休止地打印号。下面关于死循环的说法中, 只有（  A  ）是正确的。

  • 不存在一种算法, 对任何一个程序及相应的输入数据, 都可以判断是否会出现死循环, 因而, 任何编译系统都不做死循环检查
  • 有些编译系统可以检测出死循环
  • 死循环属于语法错误， 既然编译系统能检查各种语法错误， 当然也能检查出死循环
  • 死循环与多进程中出现的“死锁”差不多，而死锁是可以检测的，因而，死循环也是可以检测的
  • 对于死循环，只能等到发生时做现场处理, 没有什么更积极的手段

杂项

面向对象程序设计（Object-Oriented Programming）是一种程序设计的方法论，它将对象作为程序的基本单元，将数据和程序封装在对象中，以提高软件的重用性、灵活性和扩展性。下面关于面向对象程序设计的说法中，正确的是（ BCD ）。

  • 面向对象程序设计通常采用自顶向下设计方法进行设计。
  • 面向对象程序设计方法具有继承性（inheritance）、封装性（encapsulation）、多态性（polymorphism）等几大特点。
  • 支持面向对象特性的语言称为面向对象的编程语言，目前较为流行的有C++、JAVA、C#等。
  • 面向对象的程序设计的雏形来自于Simula语言，后来在SmallTalk语言的完善和标准化的过程中得到更多的扩展和对以前思想的重新注解。至今，SmallTalk语言仍然被视为面向对象语言的基础。

在关系数据库中, 存放在数据库中的数据的逻辑结构以( E )为主。

A. 二叉树        B. 多叉树        C. 哈希表        D. B+树      E. 二维表

命题“P→Q”可读做P蕴含Q， 其中P、Q是两个独立的命题. 只有当命题P成立而命题Q不成立时， 命题"P→Q"的值为false， 其它情况均为true. 与命题"P→Q"等价的逻辑关系式是（  AD  ）。

A. ﹁ P∨Q                B. P∧Q                    C. ﹁ (P∨Q)        D. ﹁(﹁Q∧P )

堆排序实现

前缀/后缀表达式

前缀表达式 “+ 3 * 2 + 5 12” = 37

表达式a*(b+c)-d的后缀表达式是：B

A. abcd*± B. abc+d- C. abc+d- D. -+*abcd

错题本

（矩阵中的数字）有一个 n*n(1<=n<=5000) 的矩阵 aa ， 对于 1 <= i < n , 1<=j<=n, a[i,j] < a[i + 1,j] a[j,i] < a[j,i+1]。即矩阵中左右相邻的两个元素，右边的元素一定比左边的大。上下相邻的两个元素，下面的元素一定比上面的大。给定矩阵a中的一个数字k，找出k所在的行列（注意：输入数据保证矩阵中的数各不相同）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
using namespace std;
int n,k,answerx,answery;
int a[5001][5001];

void FindKPosition()
{
	int i = n,j = n;
	while (j > 0)
	{
		if (a[n][j] < k) break;               
		j --;
	}
        ①        
	while (a[i][j] != k)
	{
		while (              ②              && i > 1) i --;
		while (              ③              && j <= n) j ++;
	}
	              ④             
	              ⑤             
}

int main()
{
	int i,j;
	cin >> n;
	for (i = 1;i <= n;i ++)
		for (j = 1;j <= n;j ++)
			cin >> a[i][j];
	cin >> k;
	FindKPosition();
	cout << answerx << " " << answery << endl;
     return 0;
}

① j++; (或者 j+=1;或者j=j+1;)
② a[i][j] > k
③ a[i][j] < k
④ answerx = i;
⑤ answery = j;

第 K 大

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <iostream>
using namespace std;

int a[1000001],n,ans = -1;
void swap(int &a,int &b)
{
	int c;
	c = a; a = b;	b = c;
}

int FindKth(int left, int right, int n)
{
	int tmp,value,i,j;
	if (left == right) return left;
	tmp = rand()% (right - left) + left;
	swap(a[tmp],a[left]);
	value =          ①         
	i = left;
	j = right;
	while (i < j)
	{
		while (i < j &&            ②        ) j --;
		if (i < j) {a[i] = a[j]; i ++;} else break;
		while (i < j &&            ③        ) i ++;
		if (i < j) {a[j] = a[i]; j --;} else break;
	}
	        ④         
	if (i < n) return  FindKth(               ⑤            );
	if (i > n) return                   ⑥                    
	return i;
}

int main()
{
	int i;
	int m = 1000000;
	for (i = 1;i <= m;i ++)
		cin >> a[i];
	cin >> n;
	ans = FindKth(1,m,n);
	cout << a[ans];
     return 0;
}

① a[left];
② a[j] < value (或a[j] <= value)
③ a[i] > value （或a[i] >= value）
④ a[i] = value;
⑤ i + 1,right,n
⑥ FindKth(left, i – 1, n);

N个人在操场里围成一圈，将这N个人按顺时针方向从1到N编号，然后从第一个人起，每隔一个人让下一个人离开操场，显然，第一轮过后，具有偶数编号的人都离开了操场。依次做下去，直到操场只剩下一个人，记这个人的编号为J(N)，例如，J(5)=3，J(10)=5，等等。

J(400) = 289         （提示：对N=2m+r进行分析，其中0≤r<2m）。

同时查找 2n2n 个数中的最大值和最小值，最小比较次数 3n−23n-2

1 到 2015 不能被 4,5,6 中任意一个数整除的数个数：1075

a,b∈[0,31]  a×b=(aor⁡b)×(aand⁡b)a,b\in[0,31]\; a\times b=(a\operatorname{or}b)\times (a\operatorname{and} b) 解的个数 454

一只小猪要买 N 件物品（N 不超过 1000）。

它要买的所有物品在两家商店里都有卖。第 i 件物品在第一家商店的价格是 a[i] ，在第二家商店的价格是 b[i] ，两个价格都不小于 0 且不超过 10000。如果在第一家商店买的物品的总额不少于 50000，那么在第一家店买的物品都可以打 95 折(价格变为原来的 0.95 倍)。

求小猪买齐所有物品所需最少的总额。

输入：第一行一个数 N。接下来N 行，每行两个数。第 i 行的两个数分别代表 a[i]，b[i]。

输出：输出一行一个数，表示最少需要的总额，保留两位小数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <cstdio>
#include <cstdlib>
using namespace std;

const int Inf = 1000000000;
const int threshold = 50000;
const int maxn = 1000;

int n, a[maxn], b[maxn];
bool put_a[maxn];
int total_a, total_b;

double ans;
int f[threshold];

int main() {
    scanf("%d", &n);
    total_a = total_b = 0;
    for (int i = 0; i < n; ++i) {
        scanf("%d%d", a + i, b + i);
        if (a[i] <= b[i]) total_a += a[i];
        else total_b += b[i];
    }
    ans = total_a + total_b;
    total_a = total_b = 0;
    for (int i = 0; i < n; ++i) {
        if ( ① ) {
            put_a[i] = true;
            total_a += a[i];
        } else {
            put_a[i] = false;
            total_b += b[i];
        }
    }
    if ( ② ) {
        printf("%.2f", total_a * 0.95 + total_b);
        return 0;
    }
    f[0] = 0;
    for (int i = 1; i < threshold; ++i)
        f[i] = Inf;
    int total_b_prefix = 0;
    for (int i = 0; i < n; ++i)
        if (!put_a[i]) {
            total_b_prefix += b[i];
            for (int j = threshold - 1; j >= 0; --j) {
                if ( ③ >= threshold && f[j] != Inf)
                    ans = min(ans, (total_a + j + a[i]) * 0.95 + ④ );
                f[j] = min(f[j] + b[i], j >= a[i] ? ⑤ : Inf);
            }
        }
    printf("%.2f", ans);
    return 0;
}

a[i]*0.95 <= b[i]
total_a >= 50000
total_a + j + a[i]
f[j] + total_b - total_b_prefix
f[j - a[i]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
using namespace std;
string s;

long long magic(int l, int r) {
    long long ans = 0;
        for (int i = l; i <= r; ++i) {
        ans = ans * 4 + s[i] - ‘a’ + 1;
    }
return ans;
}

int main() {
    cin >> s;
    int len = s.length();
    int ans = 0;
    for (int l1 = 0; l1 < len; ++l1) {
        for (int r1 = l1; r1 < len; ++r1) {
            bool bo = true;
            for (int l2 = 0; l2 < len; ++l2) {
                for (int r2 = l2; r2 < len; ++r2) {
                    if (magic(l1, r1) == magic(l2, r2) 
                    	&& (l1 != l2 || r1 != r2)) 
                    	bo = false;
                }
            }
            
            if (bo) {
                ans += 1;
            }
        }
    }
    cout << ans << endl;
    return 0;
}

input: abacaba
ouput: 16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
using namespace std;
int lps(string seq, int i, int j)
{
    int len1, len2;
    if (i == j)
        return 1;
    if (i > j)
        return 0;
    if (seq[i] == seq[j])
        return lps(seq, i + 1, j - 1) + 2;
    len1 = lps(seq, i, j - 1);
    len2 = lps(seq, i + 1, j);
    if (len1 > len2)
        return len1;
    return len2;
}
int main()
{
    string seq = "acmerandacm";
    int n = seq.size();
    cout << lps(seq, 0, n - 1) << endl;
    return 0;
}
output: 5

对下图使用Dijkstra算法计算S点到其余各点的最短路径长度时，到B点的距离d[B]初始时赋为8，在算法的执行过程中还会出现的值有（ BCD ）。

graph

A. 3 B. 7 C. 6 D. 5

关于计算机内存下面的说法哪些是正确的：BD

  • 随机存储器（RAM）的意思是当程序运行时，每次具体分配给程序的内存位置是随机而不确定的。
  • 一般的个人计算机在同一时刻只能存/取一个特定的内存单元。
  • 计算机内存严格说来包括主存（memory）、高速缓存（cache）和寄存器（register）三个部分。
  • 1MB内存通常是指1024*1024字节大小的内存。

初赛复习

https://gesrua.xyz/archives/初赛复习

作者

Gesrua

发布于

2019-10-18

更新于

2020-09-26

许可协议

#

目录

分类

×